El Método Montessori, 2ª Edición - Restauración # Capítulo 19 - Enseñanza de la numeración, la introducción de la aritmética Los niños de tres años ya saben contar hasta dos o tres cuando entran en nuestras escuelas. Por lo tanto  , aprenden ***muy fácilmente***  la numeración, que consiste  ***en contar objetos** .*  Una docena de formas diferentes pueden servir para este fin, y la vida diaria presenta muchas oportunidades; cuando la madre dice, por ejemplo, "Te faltan dos botones en el delantal" o "Necesitamos tres platos más en la mesa". Uno de los primeros medios que utilicé es el de contar con dinero. Obtengo  dinero ***nuevo***  , y si fuera posible debo tener buenas reproducciones hechas en cartón. He visto ese dinero usado en una escuela para deficientes en Londres. La  ***realización del cambio***  es una forma de numeración tan atractiva como para captar la atención del niño. Les presento las piezas de uno, dos y cuatro céntimos, y los niños, de esta forma aprenden a contar hasta  ***diez** .* Ninguna forma de instrucción es más  ***práctica***  que la que tiende a familiarizar a los niños con las monedas de uso común, y ningún ejercicio es más útil que el de dar cambio. Está tan estrechamente relacionado con la vida cotidiana que interesa intensamente a todos los niños. Habiendo enseñado la numeración en este modo empírico, paso a ejercicios más metódicos, teniendo como material didáctico uno de los juegos de bloques ya usados ​​en la educación de los sentidos; a saber, la serie de diez varillas utilizadas hasta ahora para la enseñanza de la longitud. La más corta de estas varillas corresponde a un decímetro, la más larga a un metro, mientras que las varillas intermedias se dividen en secciones de un decímetro de longitud. Las secciones están pintadas alternativamente de rojo y azul.  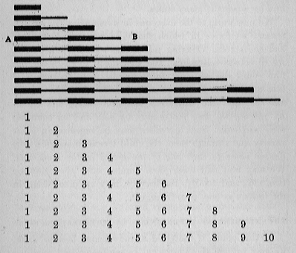Algún día, cuando un niño haya arreglado las varillas, colocándolas en orden de longitud, le hacemos contar las señales rojas y azules, comenzando con la pieza más pequeña; es decir, uno; uno dos; uno, dos, tres, etc., siempre volviendo a uno en el conteo de cada varilla, y comenzando desde el lado A. Luego le pedimos que nombre las varillas individuales de la más corta a la más larga, según el número total de secciones que cada uno contiene, tocando las varillas del lado B, por cuyo lado sube la escalera. Esto da como resultado la misma numeración que cuando contamos la varilla más larga 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Deseando saber el número de varillas, las contamos desde el lado A y lo mismo resultados de numeración; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Ahora unimos los ejercicios de  ***numeración***  con los ejercicios sensoriales anteriores en los que el niño reconocía las varillas largas y cortas. Habiendo mezclado las varillas sobre una alfombra, la directora selecciona una y, mostrándosela al niño, le pide que cuente las secciones; por ejemplo, 5. Luego le pide que le dé el siguiente en longitud. Lo selecciona  ***con el ojo*** , y la directora le pide que  ***verifique***  su elección  ***colocando las dos piezas una al lado de la otra y contando sus secciones** .*  Dichos ejercicios pueden repetirse en gran variedad ya través de ellos el niño aprende a asignar un  ***nombre particular a cada una de las piezas de la larga escalera.** .* Ahora podemos llamarlos pieza número uno; pieza número dos, etc., y finalmente, por brevedad, puede hablarse de ellos en las lecciones como uno, dos, tres, etc. ## [19.1 Números representados por signos gráficos](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.1-numbers-as-represented-by-graphic-signs 'Enlace al texto base de traducción de Montessori.Zone "El método Montessori"') En este punto, si el niño ya sabe escribir, podemos presentarle las figuras cortadas en papel de lija y montadas sobre cartulinas. En la presentación de estos, el método es el mismo que se utiliza en la enseñanza de las letras. "Este es uno." "Esto es dos". "Dame uno." "Dame dos". "¿Qué  *número*  es este?" El niño traza el número con el dedo como hizo con las letras. ***Ejercicios con Números** .*  Asociación del signo gráfico con la cantidad. He diseñado dos bandejas cada una dividida en cinco pequeños compartimentos. En la parte posterior de cada compartimento se puede colocar una tarjeta con una cifra. Las cifras en la primera bandeja deben ser 0, 1, 2, 3, 4, y en la segunda, 5, 6, 7, 8 y 9. El ejercicio es obvio; consiste en colocar dentro de los compartimentos algunos objetos correspondientes a la cifra indicada en la tarjeta en la parte posterior del compartimento. Damos a los niños varios objetos para variar la lección, pero principalmente hacemos uso de grandes clavijas de madera con forma tal que no se caigan rodando del escritorio. Colocamos un número de estos ante el niño que le corresponde colocarlos en su lugar, una clavija correspondiente a la tarjeta marcada con uno, etc. Cuando termina lleva su bandeja a la directora para que verifique su trabajo. ***La lección sobre el cero** .*  Esperamos hasta que el niño, señalando el compartimento que contiene la tarjeta marcada con cero, pregunta: "¿Y qué debo poner aquí?" Entonces respondemos: "Nada; cero es nada". Pero a menudo esto no es suficiente. Es necesario hacer  ***sentir*** al niño  lo que entendemos por  ***nada** .*  Para ello, nos valemos de pequeños juegos que entretienen enormemente a los niños. Me paro entre ellos y, dirigiéndome a uno de ellos que ya ha usado este material, le digo: "Ven, querida, ven a mí  ***cero***  veces". El niño casi siempre viene a mí y luego vuelve corriendo a su lugar. "Pero, muchacho, viniste  ***una***  vez, y te dije que vinieras  ***cero*** veces." Entonces comienza a preguntarse. "¿Pero qué debo hacer, entonces?" "Nada; cero es nada." "¿Pero cómo voy a hacer nada?" "No hagas nada. Debes quedarte quieto. No debes venir en absoluto, en ningún momento. Cero veces. Ninguna vez". Repito estos ejercicios hasta que los niños entienden, y luego se divierten inmensamente en permanecer callados cuando les llamo para que vengan a mí cero veces o para que me tiren cero besos. A menudo gritan: "Cero es ¡nada! ¡Cero no es nada!" ## [19.2 Ejercicios para la memoria de números](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.2-exercises-for-the-memory-of-numbers 'Enlace al texto base de traducción de Montessori.Zone "El método Montessori"') Cuando los niños reconozcan la figura escrita, y cuando esta figura les signifique el valor numérico, les doy el siguiente ejercicio: Recorto las cifras de viejos calendarios y las monto en tiras de papel que luego se doblan y se dejan caer en una caja. Los niños sacan los papeles y los llevan aún doblados, a sus asientos, donde los miran y los vuelven a doblar,  ***conservando el secreto** .*  Luego, uno por uno, o en grupos, estos niños (que naturalmente son los mayores de la clase) se dirigen a la mesa grande de la directora donde se han colocado grupos de varios objetos pequeños. Cada uno selecciona la  ***cantidad***  de objetos correspondiente al número que ha sorteado. El número, por su parte, se ha dejado  ***en casa del niño*** , un papelito doblado misteriosamente. El niño, por tanto, debe  ***recordar*** su número no sólo durante los movimientos que hace al ir y venir, sino mientras recoge sus piezas, contándolas una por una. La directora puede hacer aquí interesantes observaciones individuales sobre la memoria de números. Cuando el niño ha recogido sus objetos, los dispone sobre su propia mesa, en columnas de dos, y si el número es impar, coloca la pieza impar en el fondo y entre los dos últimos objetos. Por lo tanto, la disposición de las piezas es la siguiente: ``` o o o o o o o o o o X XX XX XX XX XX XX XX XX XX X XX XX XX XX XX XX XX X XX XX XX XX XX X XX XX XX X XX ``` Las cruces representan los objetos, mientras que el círculo representa la hoja doblada que contiene la figura. Habiendo arreglado sus objetos, el niño espera la verificación. Llega la directora, abre la boleta, lee el número y cuenta las piezas. Cuando jugamos este juego por primera vez, a menudo sucedía que los niños tomaban  ***más objetos***  de los que pedía la tarjeta, y esto no siempre se debía a que no recordaban el número, sino que surgía de una manía por tener la mayor cantidad de objetos. Un poco de esa codicia instintiva, que es común al hombre primitivo e inculto. La directora busca explicar a los niños que es inútil tener todas esas cosas sobre el escritorio y que el objetivo del juego es tomar la cantidad exacta de objetos que se piden. Poco a poco se van adentrando en esta idea, pero no tan fácil como se podría suponer. Es un verdadero esfuerzo de abnegación que mantiene al niño dentro del límite establecido y le hace tomar, por ejemplo, sólo dos de los objetos puestos a su disposición, mientras ve que otros toman más. Por lo tanto, considero este juego más un ejercicio de fuerza de voluntad que de numeración. El niño que tiene el  ***cero*** , no debe moverse de su lugar cuando ve a todos sus compañeros levantarse y tomar libremente de los objetos que le son inaccesibles. Muchas veces el cero cae en la suerte de un niño que sabe contar perfectamente, y que experimentaría un gran placer en acumular y disponer un buen grupo de objetos en el debido orden sobre su mesa, y en esperar con seguridad la verificación del maestro. Es muy interesante estudiar las expresiones en los rostros de aquellos que poseen cero. Las diferencias individuales que resultan son casi una revelación del "carácter" de cada uno. Algunos permanecen impasibles, asumiendo una fachada audaz para ocultar el dolor de la decepción; otros muestran esta desilusión con gestos involuntarios. Sin embargo, otros no pueden ocultar la sonrisa que les provoca la singular situación en la que se encuentran, y que despertará la curiosidad de sus amigos. Hay pequeños que siguen cada movimiento de sus compañeros con una mirada de deseo, casi de envidia, mientras que otros muestran una instantánea aceptación de la situación. No menos interesantes son las expresiones con las que confiesan la tenencia del cero cuando se les pregunta durante la verificación, "¿y tú, no te has llevado nada?". "Tengo cero". "Es cero". Estas son las palabras habituales, pero el rostro expresivo y el tono de la voz muestran sentimientos muy variados. Raros, en verdad, son aquellos que parecen dar con placer la explicación de un hecho extraordinario. La mayoría parece infeliz o simplemente resignada. Nosotros, por lo tanto, damos lecciones sobre el significado del juego, diciendo: "Es difícil guardar cero secretos. Dobla bien el papel y no dejes que se escape. Es el más difícil de todos". De hecho, después de un tiempo, la dificultad misma de permanecer callados atrae a los niños, y cuando abren el recibo marcado con un cero, se puede ver que están contentos con guardar el secreto. ## [19.3 Suma y resta de uno a veinte: multiplicación y división](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.3-addition-and-subtraction-from-one-to-twenty%3A-multiplication-and-division 'Enlace al texto base de traducción de Montessori.Zone "El método Montessori"') El material didáctico que utilizamos para la enseñanza de las primeras operaciones aritméticas es el mismo que ya se utiliza para la numeración; esto es, las varillas graduadas en longitud que, dispuestas en la escala del metro, contienen la primera idea del sistema decimal. Las varas, como he dicho, han venido a llamarse por los números que representan; uno, dos, tres, etc. Están ordenados por longitud, que también es por orden de numeración. El primer ejercicio consiste en tratar de juntar las piezas más cortas de forma que formen decenas. La forma más sencilla de hacerlo es tomar sucesivamente las varillas más cortas, de uno hacia arriba, y colocarlas al final de las correspondientes varillas largas de nueve hacia abajo. Esto puede ir acompañado de los mandatos: "Toma uno y súmalo a nueve; toma dos y súmalo a ocho; toma tres y súmalo a siete; toma cuatro y súmalo a seis". De esta forma, hacemos cuatro varillas iguales a diez. Queda el cinco, pero, volviéndolo de cabeza (en sentido largo), pasa de un extremo del diez al otro, y así aclara el hecho de que dos por cinco son diez. Estos ejercicios se repiten y poco a poco se le enseña al niño el lenguaje más técnico; nueve más uno es diez, ocho más dos es diez, siete más tres es diez, seis más cuatro es diez, y para el cinco que queda, dos por cinco es diez. Por fin, si sabe escribir, le enseñamos los signos  *más*  ,  *igual*  y  *tiempos.*  Entonces esto es lo que vemos en los pulcros cuadernos de nuestros pequeños: ``` 9+1=10 8+2=10 5x2=10 7+3=10 6+4=10 ``` Cuando todo esto está bien aprendido y los niños lo han plasmado con mucho gusto en el papel, les llamamos la atención sobre el trabajo que se realiza cuando las piezas agrupadas para formar decenas se separan y se vuelven a colocar en sus posiciones originales. De los diez últimos formados quitamos cuatro y seis restos; del siguiente, sacamos tres y siete restos; del siguiente quedan dos y ocho; del último, quitamos uno y nueve restos. Hablando de esto propiamente decimos, diez menos cuatro es igual a seis; diez menos tres es igual a siete; diez menos dos es igual a ocho; diez menos uno es igual a nueve. En cuanto a los cinco restantes, es la mitad de diez, y cortando la vara larga en dos, que es dividir diez por dos, tendríamos cinco; diez dividido por dos es igual a cinco. El registro escrito de todo esto dice: ``` 10-4=6 10-3=7 10 / 2=5 10-2=8 10-1=9 ``` Una vez que los niños dominan este ejercicio lo multiplican espontáneamente. ¿Podemos hacer tres de dos maneras? Colocamos el uno después del dos y luego escribimos, para recordar lo que hemos hecho, 2+1=3. ¿Podemos hacer dos barras iguales al número cuatro? 3+1=4 y 4-3=1; 4-1=3. La vara número dos en su relación con la vara número cuatro se trata como si fuera la cinco en relación con la diez; es decir, le damos la vuelta y mostramos que está contenido en cuatro exactamente dos veces: 4/2=2; 2x2=4. Otro problema: veamos con cuántas cañas podemos jugar a este mismo juego. Podemos hacerlo con tres y seis, y con cuatro y ocho; eso es, ``` 2x2=4 3x2=6 4x2=8 5x2=10 10/2=5 8/2=4 6/2=3 4/2=2 ``` En este punto encontramos que los cubos con los que jugamos los juegos de memoria de números son de ayuda:  A partir de esta disposición, se ve de inmediato cuáles son los números que se pueden dividir por dos, todos aquellos que no tienen un cubo impar en la parte inferior. Estos son los  números ***pares***  porque se pueden ordenar en pares, de dos en dos; y la división por dos es fácil, basta con separar las dos filas de dos que están una debajo de la otra. Contando los cubos de cada archivo tenemos el cociente. Para recomponer el número primitivo, solo necesitamos volver a ensamblar los dos archivos, por lo tanto, 2x3 = 6. Todo esto no es difícil para los niños de cinco años. La repetición pronto se vuelve monótona, pero los ejercicios pueden cambiarse más fácilmente, tomando de nuevo el juego de varillas largas, y en lugar de colocar la varilla número uno después de la nueve, colóquela después de la diez. De la misma manera, coloque dos después de las nueve y tres después de las ocho. De esta manera hacemos varillas de una longitud mayor que diez; longitudes que debemos aprender a nombrar once, doce, trece, etc., hasta veinte. Los pequeños cubos también pueden usarse para fijar estos números más altos. Habiendo aprendido las operaciones hasta el diez, procedemos sin dificultad hasta el veinte. La única dificultad radica en los  ***números decimales***  que requieren ciertas lecciones. ## [19.4 Lecciones sobre decimales: cálculos aritméticos más allá de diez](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.4-lessons-on-decimals%3A-arithmetical-calculations-beyond-ten 'Enlace al texto base de traducción de Montessori.Zone "El método Montessori"') El material didáctico necesario consiste en una serie de tarjetas cuadradas en las que se imprime el número diez en letra grande, y otras tarjetas rectangulares, de la mitad del tamaño del cuadrado, y que contienen los números individuales del uno al nueve. Colocamos los números en una línea; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Luego, al no tener más números, debemos comenzar de nuevo y tomar el 1 nuevamente. Este 1 es como esa sección en el juego de varillas que, en la varilla número 10, se extiende más allá de nueve. Contando a lo largo  ***de la escalera*** hasta el nueve, queda esta única sección que, como no hay más números, designamos de nuevo como 1; pero este es un 1 mayor que el primero, y para distinguirlo del primero ponemos cerca de él un cero, signo que no significa nada. Aquí entonces está el 10. Cubriendo el cero con las tarjetas numéricas rectangulares separadas en el orden de su sucesión, vemos formados: 11, 12, 13, 14, 15, 16, 17, 18, 19. Estos números se componen sumando a la barra número 10, primera varilla número 1, luego 2, luego 3, etc., hasta que finalmente sumamos la varilla número 9 a la varilla número 10, obteniendo así una varilla muy larga, que al contar alternando tramos rojos y azules, da nosotros diecinueve.  La directora puede entonces mostrarle al niño las cartas, dándole el número 16, y él puede colocar la barra 6 después de la barra 10. Luego quita la tarjeta que lleva el 6 y coloca sobre el cero la tarjeta que lleva la cifra 8, con lo cual el niño quita la barra 6 y la reemplaza con la barra 8, haciendo así 18. Cada uno de estos actos puede registrarse así: 10+6=16; 10+8=18, etc. Se procede de la misma forma a la resta. 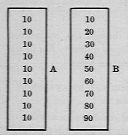Cuando el número en sí comienza a tener un significado claro para el niño, las combinaciones se hacen sobre una tarjeta larga, colocando las tarjetas rectangulares que llevan las nueve cifras sobre las dos columnas de números que se muestran en las figuras A y B. Sobre la carta A superponemos al cero del segundo 10, la carta rectangular que lleva el 1: y debajo de esta la que lleva el dos, etc. Así, mientras uno de los diez permanece igual, los números a la derecha van del cero al nueve, de este modo:  En la tarjeta B las aplicaciones son más complejas. Las cartas se superponen en progresión numérica por decenas. Casi todos nuestros niños cuentan hasta 100, número que les fue dado en respuesta a la curiosidad que mostraban por aprenderlo. No creo que esta fase de la enseñanza necesite más ilustraciones. Cada maestro podrá multiplicar los ejercicios prácticos en las operaciones aritméticas, utilizando objetos sencillos que los niños puedan manejar y dividir fácilmente. > ##### **La Licencia de esta página:** > > Esta página es parte del “ **Proyecto Montessori de Restauración y Traducción** ”.\ > Apoye nuestra [iniciativa " ](https://ko-fi.com/montessori)**Educación Montessori todo incluido para todos 0-100+ en todo el mundo** ". Creamos recursos abiertos, gratuitos y asequibles disponibles para todos los interesados ​​en la educación Montessori. Transformamos personas y entornos para que sean auténticos Montessori en todo el mundo. ¡Gracias! > > [](http://creativecommons.org/licenses/by-nc-sa/4.0/) > > **Licencia:** Este trabajo con todas sus ediciones de restauración y traducciones tiene una  [licencia internacional Creative Commons Attribution-NonCommercial-ShareAlike 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) . > > Consulte el **Historial** de la página de cada página wiki en la columna de la derecha para obtener más información sobre todos los colaboradores y las ediciones, restauraciones y traducciones realizadas en esta página. > > [¡ Las contribuciones](https://ko-fi.com/montessori) y los [patrocinadores](https://ko-fi.com/montessori) son bienvenidos y muy apreciados! * [El método Montessori, 2ª edición](https://montessori-international.com/s/the-montessori-method/wiki/Spanish "El Método Montessori en la Zona Montessori - Idioma Inglés") - Restauración Española - [Archive.Org](https://archive.org/details/montessorimethod00montuoft/ "El Método Montessori en Aechive.Org") - [Biblioteca abierta](https://openlibrary.org/books/OL7089223M/The_Montessori_method "El método Montessori en Open Library") * [0 - Índice de capítulos - El método Montessori, 2ª edición - Restauración - Biblioteca abierta](https://montessori-international.com/s/the-montessori-method/wiki/0+-+%C3%8Dndice+de+cap%C3%ADtulos+-+El+m%C3%A9todo+Montessori%2C+2%C2%AA+edici%C3%B3n+-+Restauraci%C3%B3n+-+Biblioteca+abierta) * [Capítulo 00 - Dedicatoria, Agradecimientos, Prefacio a la Edición Americana, Introducción](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+00+-+Dedicatoria%2C+Agradecimientos%2C+Prefacio+a+la+Edici%C3%B3n+Americana%2C+Introducci%C3%B3n) * [Capítulo 01 - Una consideración crítica de la nueva pedagogía en su relación con la ciencia moderna](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+01+-+Una+consideraci%C3%B3n+cr%C3%ADtica+de+la+nueva+pedagog%C3%ADa+en+su+relaci%C3%B3n+con+la+ciencia+moderna) * [Capítulo 02 - Historia de los métodos](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+02+-+Historia+de+los+m%C3%A9todos) * [Capítulo 03 - Discurso inaugural pronunciado con motivo de la inauguración de una de las “Casas de los Niños”](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+03+-+Discurso+inaugural+pronunciado+con+motivo+de+la+inauguraci%C3%B3n+de+una+de+las+%E2%80%9CCasas+de+los+Ni%C3%B1os%E2%80%9D) * [Capítulo 04 - Métodos Pedagógicos utilizados en las “Casas de Niños”](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+04+-+M%C3%A9todos+Pedag%C3%B3gicos+utilizados+en+las+%E2%80%9CCasas+de+Ni%C3%B1os%E2%80%9D) * [Capítulo 05 - Disciplina](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+05+-+Disciplina) * [Capítulo 06 - Cómo se debe dar la lección](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+06+-+C%C3%B3mo+se+debe+dar+la+lecci%C3%B3n) * [Capítulo 07 - Ejercicios para la vida práctica](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+07+-+Ejercicios+para+la+vida+pr%C3%A1ctica) * [Capítulo 08 - Reflexión de la dieta del Niño](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+08+-+Reflexi%C3%B3n+de+la+dieta+del+Ni%C3%B1o) * [Capítulo 09 - Gimnasia de educación muscular](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+09+-+Gimnasia+de+educaci%C3%B3n+muscular) * [Capítulo 10 - Naturaleza en la educación laboral agrícola: Cultivo de plantas y animales](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+10+-+Naturaleza+en+la+educaci%C3%B3n+laboral+agr%C3%ADcola%3A+Cultivo+de+plantas+y+animales) * [Capítulo 11 - Trabajo manual el arte del alfarero y la construcción](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+11+-+Trabajo+manual+el+arte+del+alfarero+y+la+construcci%C3%B3n) * [Capítulo 12 - Educación de los sentidos](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+12+-+Educaci%C3%B3n+de+los+sentidos) * [Capítulo 13 - Educación de los sentidos e ilustraciones del material didáctico: Sensibilidad general: Los sentidos táctil, térmico, básico y estereognóstico](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+13+-+Educaci%C3%B3n+de+los+sentidos+e+ilustraciones+del+material+did%C3%A1ctico%3A+Sensibilidad+general%3A+Los+sentidos+t%C3%A1ctil%2C+t%C3%A9rmico%2C+b%C3%A1sico+y+estereogn%C3%B3stico) * [Capítulo 14 - Notas generales sobre la educación de los sentidos](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+14+-+Notas+generales+sobre+la+educaci%C3%B3n+de+los+sentidos) * [Capítulo 15 - Educación intelectual](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+15+-+Educaci%C3%B3n+intelectual) * [Capítulo 16 - Método para la enseñanza de la lectura y la escritura](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+16+-+M%C3%A9todo+para+la+ense%C3%B1anza+de+la+lectura+y+la+escritura) * [Capítulo 17 - Descripción del método y material didáctico utilizado](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+17+-+Descripci%C3%B3n+del+m%C3%A9todo+y+material+did%C3%A1ctico+utilizado) * [Capítulo 18 - El lenguaje en la infancia](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+18+-+El+lenguaje+en+la+infancia) * [Capítulo 19 - Enseñanza de la numeración: Introducción a la aritmética](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+19+-+Ense%C3%B1anza+de+la+numeraci%C3%B3n%3A+Introducci%C3%B3n+a+la+aritm%C3%A9tica) * [Capítulo 20 - Secuencia de ejercicio](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+20+-+Secuencia+de+ejercicio) * [Capítulo 21 - Revisión general de la disciplina](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+21+-+Revisi%C3%B3n+general+de+la+disciplina) * [Capítulo 22 - Conclusiones e impresiones](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+22+-+Conclusiones+e+impresiones) * [Capítulo 23 - Ilustraciones](https://montessori-international.com/s/the-montessori-method/wiki/Cap%C3%ADtulo+23+-+Ilustraciones)